Diamond Girdles

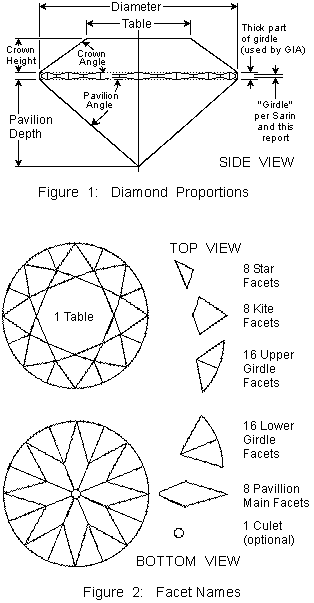
Note 1:
This article shows how adding a girdle changes Marcel Tolkowsky's Diamond Design. To avoid redundant explanations and definitions, it is meant to be read along with the web edition of Diamond Design, as edited by Jasper Paulsen.

Marcel Tolkowsky's Diamond Design shows a graphical way to determine the best crown angle and table angle for a given pavilion angle and a knife-edge girdle. The web edition of Diamond Design derives formulas for the crown angle and table size, so that a computer can use Tolkowsky's model. This author (Jasper Paulsen) edited the web edition of Diamond Design. I derived the formulas directly from Tolkowsky's model. I kept all of the assumptions and logic. This means that the formulas in the web edition also assume a knife-edge girdle.

Tolkowsky mentions the girdle. He even says that the diamond is circular. But he does not include the thickness of the girdle in the total depth of the diamond. To finish the diamond design, we need to estimate the thickness of the girdle, and determine how the girdle affects the crown angle and table size.

Note 2:
This article makes only small changes to Tolkowsky's pictures and analysis.

• Notes 3- 9 derive the formulas for girdle thickness.
  
• Notes 10-12 show the changes to Tolkowsky's pictures, and explain which variables are affected.
  
• Notes 13-22 show how much these variables are affected.
• Note 23 shows the revised formulas.
• Notes 24-25 graph the results, for various girdle sizes.
• Notes 26-27 tabulate the results, for various girdle sizes.
• Note 28 links to other sites with more information.

Note 3:
Tolkowsky mentions the girdle. He says that "With the introduction of mechanical bruting or cutting (an operation distinct from polishing ; see p. 17) diamonds were made absolutely circular in plan (fig. 37)." Figure 37 shows a circular diamond, not a 16-sided diamond. Tolkowsky even mentions girdle thickness, when he says, "Where the cut is somewhat less fine and the girdle is somewhat thick (to save weight)," the lower girdle faceting is affected. But Tolkowsky does not include the thickness of the girdle in the total depth of the diamond. We need to estimate the thickness of the girdle.

Note 4:
As shown in fig. 1, our calculations need the total thickness of the girdle. Similarly, GIA studies (and descriptions of diamonds) use the total thickness of the girdle (at the "mains"). But most of the real-world data about diamonds (e.g., from Sarin machines, AGS certificates, and on-line ads) reports the thin part of the girdle (at the "scallops").

To make this article as useful as possible in the real world, we will use the Sarin definition of the "girdle": "The average thickness of the thin parts of the girdle" (at the "scallops"). We will calculate the size of the "Girdle Wave". By adding the "girdle" and "Girdle Wave", we can find the total thickness of the girdle (at the "mains").

The girdle has three layers.

1. At the top: The upper girdle facets (in the crown) extend below the tips of the kite facets.
2. In the middle: The outer edge of the girdle is a circle. The girdle is thinnest (at the "scallops") between the bottoms of the upper girdle facets and the tops of the lower girdle facets. Sarin machines call this distance the "girdle thickness".
3. At the bottom: The lower girdle facets (in the pavilion) extend above the tips of the pavilion main facets.

The "Girdle Wave" is the thickness of the top layer of the girdle plus the bottom layer of the girdle.

Note 5:
The middle layer can be any thickness at all. Sarin machines measure it and call it the "girdle thickness". Often the "girdle thickness" is between 0.7% and 2% of the diameter of medium-sized and large diamonds. (Small diamonds usually have a larger percentage girdle.)

Note 6:
The thickness of the top and bottom layers depends on the difference between a diamond with a "knife edge girdle" and a diamond with a circular girdle.

A diamond with a "knife edge girdle" has no girdle at all. But without a girdle, the diamond is a 16-sided polygon, not a circle. A 16-sided polygon does not have the same radius all the way around. The minimum radius of the sixteen-sided polygon is:
        DiamondRadius * cos (11° 15')
     =  diameter / 2  * cos (11° 15')

When the girdle is circular, the upper and lower girdle facets run out from the 16-sided polygon to the circular girdle. The slopes have a run of:
        DiamondRadius - MinimumRadius
     =  diameter / 2  - diameter / 2 * cos (11° 15')
     =  diameter / 2  * (1 - cos (11° 15'))

Note 7:
Tolkowsky says the upper girdle facet should have an angle of 42°. The slope (rise over run) is tan 42°. The thickness of the upper layer of the girdle is:
        (Run from 16-sided polygon to circle) * (Slope of facet)
     =  diameter / 2 * (1 - cos (11° 15')) * tan 42°
     =  diameter * 0.00865

Actually, the upper girdle facet angle is closer to 39°,
to let the kite facet have 4 sides.
This increases the thickness of the upper layer of the girdle
from diameter * 0.00865 to diameter * 0.00885
We will neglect this error of diameter * 0.0002 .

Note 8:
Let alpha be the pavillion angle. Tolkowsky says the lower girdle facet should have an angle of alpha + 2°. The thickness of the lower layer of the girdle is:
        (Run from 16-sided polygon to circle) * (Slope of facet)
     =  diameter / 2 * (1 - cos (11° 15')) * tan (alpha + 2°)
For alpha = 40° 45', this is:
     =  diameter / 2 * (1 - cos (11° 15')) * tan (42° 45')
     =  diameter * 0.00888

Note 9:
The girdle is thickest at the tips of the kite facets and lower girdle facets.
This distance is shown in fig. 3 as E_crown  E_pav
The total thickness of all three layers of the girdle is:
  E_crownE_pav  =  diameter * (girdle + ½ * (1 - cos (11° 15')) * (tan 42° + tan (alpha + 2°)))
Let
         v  =                      ½ * (1 - cos (11° 15')) * (tan 42° + tan (alpha + 2°))
  E_crownE_pav  =  diameter * (girdle + v)
For alpha = 40° 45', this is:
  E_crownE_pav  =  diameter * (girdle + 0.01753)

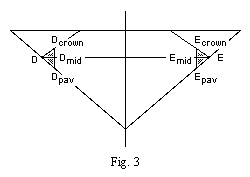
Note 10:
Fig. 3 is a simpler version of Tolkowsky's fig. 35, with a girdle. Fig. 3 shows a 10% girdle, which is very thick, so that it is easy to see. (At E_crown E_pav the thickness is 11.75%.) Most real girdles are much smaller.
D and E are on Tolkowsky's (16-sided) knife edge girdle.
The perimeter of the diamond has been trimmed, so that D_crown D_pav and E_crown E_pav are now on the outer surface.
D_mid and E_mid are the points on the girdle at the same height as D and E.

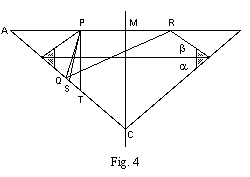
Note 11:
Fig. 4 is a simpler version of Tolkowsky's fig. 35, showing the points and rays that are NOT changed. Because points P and R are still where the table meets the kite facets, the rays that go to and from them are not changed. Thus, points Q, S, and T are unchanged. Points A and C are unchanged. Also, the definitions of alpha and beta are unchanged.

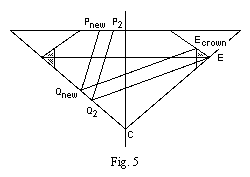
Note 12:
Fig. 5 is a simpler version of Tolkowsky's fig. 35, showing the ray that is changed. In Tolkowsky's model, ray P₂ Q₂ E was defined as the "limit for the once-reflected [average] oblique ray" that exits at the bottom of the kite facet. Since the kite face now ends at E_crown instead of E, we need to adjust the ray. The new ray is P_new Q_new E_crown. When we calculate the crown angle, we need to use Q_new C instead of Q₂ C.

Note 13:
We need to change the formulas in the editor's notes of Diamond Design. The size of the changes depends on the amount of material removed to make the girdle. The following dimensions are affected:

• We need to use Q_new C instead of Q₂ C.
• The diameter.
• The table ratio.

Note 14:
How much material is removed from the diamond?

Note 9 shows that:
  E_crownE_pav  =  diameter * (girdle + ½ * (1 - cos (11° 15')) * (tan 42° + tan (alpha + 2°)))

The triangle E_pav E_crown E is split by E_mid E. This will help us locate E_crown relative to E.
  E_pavE_mid  = E_midE * tan alpha
  E_midE_crown  = E_midE * tan beta
  E_pavE_crown  = E_pavE_mid + E_midE_crown
          = E_midE * tan alpha + E_midE * tan beta
          = E_midE * (tan alpha + tan beta)
  E_midE  =  E_pavE_crown / (tan alpha + tan beta)
  E_midE_crown  = E_midE * tan beta
          = E_pavE_crown * tan beta / (tan alpha + tan beta)

Note 15:
In the editor's notes of Diamond Design, the diameter of the finished stone is diameter. diameter cancels out of Diamond Design's angle and table ratio calculations. This means that its exact definition in Diamond Design does not matter in this article. Even if this article uses a slightly different definition of diameter, the difference will not cause a contradiction with Diamond Design.

In notes 3-9 of this article, the diameter of the finished stone is also called diameter.
  diameter  =  D_crownE_crown
            =  DE - 2 * E_midE
            =  DE - 2 * E_pavE_crown / (tan alpha + tan beta)
            =  DE - 2 * diameter * (girdle + v) / (tan alpha + tan beta)

Note 16:
The table ratio (of the girdled diamond) is:
  TableRatio  =  (PR) / (D_crownE_crown)
In the editor's notes of Diamond Design,
the table ratio (of the knife-edge diamond) is:
  t  =  PR / DE

Note 17:
If we keep this definition of t, we can re-use most of the math in the editor's notes of Diamond Design. But we will need to remember that t is NOT the table ratio of the girdled diamond. After we have calculated the crown angle and t, we will need to calculate the TableRatio of the girdled diamond.
  TableRatio  =  (PR) / diameter

Note 18:
We need to use Q_new C instead of Q₂ C. We use the horizontal offset between Q_new E_crown and Q₂ E to find Q_new C.

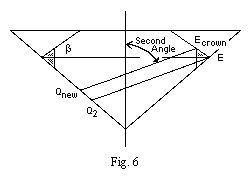
Note 19:
Fig. 6 is a simpler version of Figure 5.
Q_new E_crown is parallel to Q₂ E. It has two offsets from Q₂ E:

• E_crown is to the left of E by E_midE.
• E_crown is above E by E_midE_crown

The editor's notes to Diamond Design define the SecondAngle.
The SecondAngle is between Q₂E and the vertical.
The angle between Q₂ E and the horizontal is:
    =  90° - SecondAngle.
Since Q_new E_crown is parallel to Q₂ E,
the angle between Q_new E_crown and the horizontal is also:
    =  90° - SecondAngle.
The vertical offset of E_crown is equivalent to a horizontal offset of:
    =  E_midE_crown / tan (90° - SecondAngle)
    =  E_midE_crown * tan SecondAngle

The total horizontal offset between the parallel rays is:
    =  E_midE_crown * tan SecondAngle + E_midE
Note 14 shows that:
  E_midE_crown  =  E_midE * tan beta
The total horizontal offset between the parallel rays is:
    =  E_midE * tan beta * tan SecondAngle + E_midE
    =  E_midE * (1 + tan beta * tan SecondAngle)

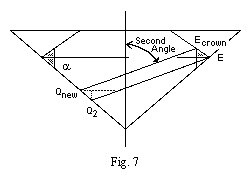
Note 20:
Fig. 7 is a simple version of Figure 5.
The ray Q₂E travels to the right as it is rises to the level of Q_new. This means that the horizontal offset between Q_new and Q₂ is less than the horizontal offset between the rays. We can split triangles again to find the horizontal offset between Q_new and Q₂. Let:
  u  =  tan (90 - alpha) / (tan (90 - alpha) + tan SecondAngle)
Then the horizontal offset between Q_new and Q₂ is:
    =  u * (the horizontal offset between the rays)
    =  u * E_midE * (1 + tan beta * tan SecondAngle)
    =  E_midE * u * (1 + tan beta * tan SecondAngle)

Note 22:
The distance along the pavilion between Q_new and Q₂ is:
  Q_newQ₂  =       E_midE * u * (1 + tan beta * tan SecondAngle) / cos alpha
so
  Q_newC   = Q₂C + E_midE * u * (1 + tan beta * tan SecondAngle) / cos alpha

Note 23:
Note 23 combines the changes listed in notes 10-22 with the formulas in editor's note 36 of Diamond Design. The variable names are defined in the editor's notes of Diamond Design. The changes are highlighted.

These formulas start with a pavilion angle (alpha) and a guess at the crown angle (beta). Then we need to loop through the formulas a few times to find the best crown angle and table ratio for the pavilion angle.

Then we will need to make sure that the diamond really is pretty. Editor's notes 30-34 of Diamond Design explain that some combinations of proportions that satisfy this model make fish-eye or nail-head diamonds, which are NOT ideal. And of course, the only way to judge if the diamond really is beautiful is to look at it in appropriate light.

Start.
We choose alpha.
We start with a guess for beta (say, 35°).

Step 1. We look at the girdle:
  DE  =  diameter of a knife-edge diamond. (1 mm is easiest.)
girdle = (thickness of narrow part of girdle) / diameter  (if it is NOT a knife-edge).
   v  =  ½ * (1 - cos (11° 15')) * (tan 42° + tan (alpha + 2°))
E_pavE_crown  =  diameter * (girdle + v)

Step 2. We find out what fraction of the oblique rays are effective, and their average angle:
        CriticalAngle         =  arcsin(1 / 2.417)   =   24° 26' 23"
        EffectiveAngle        =  arcsin(sin (alpha - 24° 26' 23") * 2.417)
        EffectiveFraction     =  [1/3 - sin(EffectiveAngle)] * 3 / (-2)
SPT  =  AverageRefractedAngle =  arcsin(( (1/3) + sin(EffectiveAngle) ) / 2 / 2.417)

Step 3. We calculate angles of rays:
 QPT  =  alpha - 24° 26' 23"
 QRP  =  90° - 2 * alpha + QPT
Q₂ED  =  90° - 2 * alpha + AverageRefractedAngle

Step 4. We calculate angles of typical rays before they leave the crown.
The FirstAngle is the angle between R'S' and the vertical.
The SecondAngle is the angle between Q₁R₁ and the vertical.
   FirstAngle   =  180° - 4 * alpha
  SecondAngle   =  2 * alpha - AverageRefractedAngle

Step 5. We calculate some ratios that make the calculations easier.
   f  =  1 + (1 / tan QPT / tan alpha)
   g  =  (1 / tan QPT - tan QRP) / 2 / tan QRP
   u  =  tan (90° - alpha) / (tan (90° - alpha) + tan SecondAngle)

Step 6. The loop starts here.
We calculate the table ratio of a knife-edge diamond:
   h  =  1 + tan beta / tan alpha
   t  =  g * h / (f + g * h)

Step 7. We calculate horizontal distances:
  PM  =  (DE / 2) * t
  AP  =  PM * f / g
E_midE  =  E_pavE_crown / (tan alpha + tan beta)

Step 8. We calculate distances along the pavilion edge:
  TC  =  PM / cos alpha
  SC  =  TC + AP * (tan SPT) / (tan SPT + 1 / tan alpha) / cos alpha
 Q₂C  =  (DE / 2) / cos alpha * (tan alpha - tan Q₂ED) / (tan alpha + tan Q₂ED)
Q_newC  =  Q₂C + E_midE * u * (1 + tan beta * tan SecondAngle) / cos alpha

Step 9. We calculate a new guess for beta (the crown angle).
   FirstWeight  =  (TC * TC)
  SecondWeight  =  EffectiveFraction * (SC * SC - Q_newC * Q_newC)

  beta = (FirstWeight * FirstAngle + SecondWeight * SecondAngle) / (FirstWeight + SecondWeight)

This gives us a new guess for beta.
The loop ends here. We can repeat steps 6-9 until the guess for beta stops changing.


Step 10. We adjust the diameter and table ratio.
          w  =  1 + 2 * (girdle + v) / (tan alpha + tan beta)
  diameter   =  DE / w
  TableRatio =   t * w

Step 11. Tolkowsky says that:

• The star facets should have about a 15° angle.
• The upper girdle facets should be at a 42° angle.
• The lower girdle facets should be 2° steeper than the pavilion main facets.

• The star facets can have a 19° or 20° angle,
  but not a 15° angle, given Tolkowsky's other proportions.
• The upper girdle facets can have a 39° angle,
  but not a 42° angle, given Tolkowsky's other proportions.

Modern diamonds have longer lower girdle facets, so these angles are slightly different.

Step 12. The diamond's total depth contains:
  CrownHeight   =  diameter / 2 * (1 - TableRatio) * tan beta
  PavilionDepth =  diameter / 2 * tan alpha
  ThinGirdle    =  diameter * girdle
  GirdleWave    =  diameter / 2 * (1 - cos (11° 15')) * (tan 42° + tan (alpha + 2°))
-(CuletHeight)  =-((culet / 2) * cos(22° 30') * tan alpha)
  TotalDepth   =  CrownHeight + PavilionDepth + ThinGirdle + GirdleWave - CuletHeight

Note 24:
Figure 8 (below) compares three sets of results:

1. Tolkowsky used a geometric model to find the best crown angle and table ratio for one pavilion angle. After rounding errors, he came up with:
   • a pavilion angle of 40° 45'
   • a crown angle of 34° 30'
   • a table ratio of 53%.
     (The table ratio is the largest diameter of the table divided by the average diameter of the diamond.)
   This point is starred (*) in figure 8.
2. My editor's notes to Diamond Design correct Tolkowsky's rounding errors, and show how the best crown angle and table ratio depend on the pavilion angle. These results are shown by the bold curves in figure 8. Unfortunately, the bold curves still use a knife-edge girdle.
3. This girdle article shows how adding a girdle changes Tolkowsky's Diamond Design.
   • The thin curves in figure 8 show diamonds whose thin parts of the girdle are 0.0 % of their diameter (at the "scallops"), and whose thick parts of the girdle are 1.7 % of their diameter (at the "mains"). These diamonds are fragile, because of their thin girdles.
   • The long-dashed curves in figure 8 show diamonds whose thin parts of the girdle are 1.0 % of their diameter (at the "scallops"), and whose thick parts of the girdle are 2.7 % of their diameter (at the "mains"). These girdles are nearly ideal for large diamonds. (They are "medium" for 6.0 mm to 8.0 mm diameters, and "slightly thick" above 8.0 mm diameters.)
   • The short-dashed curves in figure 8 show diamonds whose thin parts of the girdle are 2.0 % of their diameter (at the "scallops"), and whose thick parts of the girdle are 3.7 % of their diameter (at the "mains"). These girdles are "thick" for large diamonds, but are nearly ideal for medium-sized diamonds. (They are "medium" for 4.3 mm to 5.7 mm diameters, and "slightly thick" for 5.7 mm to 6.6 mm diameters.)
     
     To keep a constant total girdle thickness (at the thick parts = "mains"), small diamonds need a larger percentage girdle thickness. Martin Haske has posted more information about diamond girdles at: http://www.gis.net/~adamas/cut.html#girdle

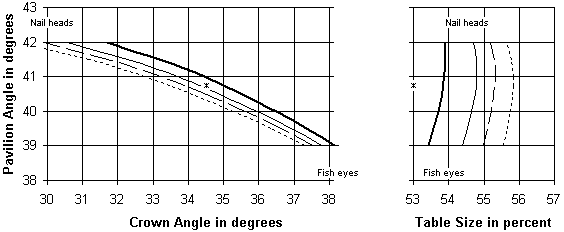
Note 25:
Figure 8 was calculated using the formulas in note 23 above, and the formulas in editor's note 36 of Diamond Design. Computer programs performed the calculations. This software lets you change the pavilion angle and girdle thickness, and see the effect on the crown angle and table ratio: http://www.folds.net/diamond.

The values are tabulated in notes 26-27. Some conclusions:

1. The differences between the stars (*) and the bold curves are due to Tolkowsky's rounding errors. Tolkowsky's rounding error on the crown angle partly offsets his error from using a knife-edge girdle. Tolkowsky's rounding error on the table size seems to go in the wrong direction.
2. The thin curves and the dashed curves show "How Adding a Girdle Changes Marcel Tolkowsky's Diamond Design." My model assumes that the thickness of the "girdle" and "Girdle Wave" reduces the brilliance of the diamond. To partly offset this, the crown is made thinner, both by reducing the crown angle and increasing the table size.
3. Figure 8 broadly agrees with actual diamonds, and with 3-D computer simulations by Moscow State University, the Gemological Institute of America, and Garry Holloway. The simulations agree that a larger pavilion angle can be offset by a smaller crown angle. (The simulations suggest slightly different pavilion angles. The differences are similar to Tolkowsky's rounding error.)
4. Caution: The model breaks down at both ends of the range.
   Editor's notes 30-34 shows that some diamonds that match the formulas are NOT ideal.
   • Extrapolating to smaller pavilion angles makes fish-eyes.
   • Extrapolating to larger pavilion angles makes nail-heads.

If you have evidence that any part of any curve on this graph describes poor diamonds, please let me know.

Note 26:
This table is copied from editor's note 37 of Diamond Design. It shows some combinations of alpha, beta, and t calculated using editor's note 36 of Diamond Design. The bold curves in fig. 8 were drawn using this table. The CrossSection.class program did the calculations: http://www.folds.net/diamond

The total depth ratio is also shown. The total depth ratio is the overall depth of the diamond divided by the diameter. It includes an adjustment for the culet facet. Because Tolkowsky's geometric model of the crown has a knife-edge girdle all the way around the diamond, there are no adjustments for the girdle.

knife-edge girdle (all the way around)
  Pavilion   Crown     Table       Total Depth Ratio
  39°        38°  9'   0.534       0.405 + 0.183 - culet ht = 0.588 - culet ht
  40°        36° 30'   0.537       0.420 + 0.171 - culet ht = 0.591 - culet ht
  40° 45'    35°  1'   0.539       0.431 + 0.162 - culet ht = 0.592 - culet ht
  41°        34° 27'   0.539       0.435 + 0.158 - culet ht = 0.593 - culet ht
  42°        31° 41'   0.539       0.450 + 0.143 - culet ht = 0.593 - culet ht

Caution: The model breaks down at both ends of this range. Editor's notes 30-34 of Diamond Design shows that some diamonds that match the formulas are NOT ideal. Extrapolating to smaller pavilion angles makes fish-eyes. Extrapolating to larger pavilion angles makes nail-heads. If you have evidence that a row of parameters (in this table) describes poor diamonds, please let me know.

Note 27:
These tables show some combinations of alpha, beta, and TableRatio calculated using note 23, above. The thin curves and dashed curves in fig. 8 were drawn using these tables. The GirdledSection.class program did the calculations: http://www.folds.net/diamond

The total depth ratio is also shown. The total depth ratio is the overall depth of the diamond divided by the diameter. It includes an adjustment for the culet facet. It also has two adjustments for the girdle: one adjustment is for the nominal girdle thickness (at its thin parts = "scallops"), and the other adjustment is for the waviness of the girdle.

The thinnest parts of a 0% girdle are knife-edges (at the "scallops").
But a 0% girdle is NOT a knife-edge all the way around.
0% girdle
  Pavilion   Crown     Table       Total Depth Ratio
  39°        37° 46'   0.544       0.405 + 0.177 + 0.017 + girdle - culet ht = 0.599 - culet ht
  40°        35° 57'   0.547       0.420 + 0.164 + 0.017 + girdle - culet ht = 0.601 - culet ht
  40° 45'    34° 18'   0.548       0.431 + 0.154 + 0.018 + girdle - culet ht = 0.603 - culet ht
  41°        33° 41'   0.548       0.435 + 0.151 + 0.018 + girdle - culet ht = 0.603 - culet ht
  42°        30° 35'   0.547       0.450 + 0.134 + 0.018 + girdle - culet ht = 0.602 - culet ht

1% girdle
  Pavilion   Crown     Table       Total Depth Ratio
  39°        37° 32'   0.55        0.405 + 0.173 + 0.017 + girdle - culet ht = 0.605 - culet ht
  40°        35° 38'   0.552       0.420 + 0.16  + 0.017 + girdle - culet ht = 0.607 - culet ht
  40° 45'    33° 53'   0.553       0.431 + 0.15  + 0.018 + girdle - culet ht = 0.609 - culet ht
  41°        33° 13'   0.553       0.435 + 0.146 + 0.018 + girdle - culet ht = 0.609 - culet ht
  42°        29° 56'   0.552       0.450 + 0.129 + 0.018 + girdle - culet ht = 0.607 - culet ht

2% girdle
  Pavilion   Crown     Table       Total Depth Ratio
  39°        37° 17'   0.556       0.405 + 0.169 + 0.017 + girdle - culet ht = 0.611 - culet ht
  40°        35° 17'   0.558       0.420 + 0.157 + 0.017 + girdle - culet ht = 0.613 - culet ht
  40° 45'    33° 27'   0.558       0.431 + 0.146 + 0.018 + girdle - culet ht = 0.614 - culet ht
  41°        32° 45'   0.558       0.435 + 0.142 + 0.018 + girdle - culet ht = 0.614 - culet ht
  42°        29° 15'   0.557       0.45  + 0.124 + 0.018 + girdle - culet ht = 0.612 - culet ht

Caution: The model breaks down at both ends of this range. Editor's notes 30-34 of Diamond Design shows that some diamonds that match the formulas are NOT ideal. Extrapolating to smaller pavilion angles makes fish-eyes. Extrapolating to larger pavilion angles makes nail-heads. If you have evidence that a row of parameters (in these tables) describes poor diamonds, please let me know.

Note 28:
This model does not include all features of real diamonds. The editor's notes of Diamond Design discuss the limitations of this model.

A computer performed the calculations in this appendix. Jasper Paulsen (the editor of this book) created the software, and posted it at FOLDS.NET. This software lets you change the pavilion angle and girdle thickness, and see the effect on crown angle, and table ratio:
http://www.folds.net/diamond

This software can be used to calculate other combinations of proportions that also satisfy this model. Unfortunately, some of these proportions do not result in ideal diamonds. Two problems are fish-eye diamonds and nail-head diamonds. These problems are described in more detail in the editor's notes of Diamond Design.

The editor's notes of Diamond Design compare these results to the results of other computer models of diamonds. The "corrected theory" column in Table II of Diamond Design compares these results with Tolkowsky's example diamonds.

Acknowledgements: I thank the late Marcel Tolkowsky for writing Diamond Design. I thank everyone kind enough to criticize this web page, and tell me things that I should fix. Garry Holloway, Marvin Leib, Bruce Harding, Martin Haske, Jefferson Lewis, and Thomas Kabele have pointed out errors and omissions. If you notice one, please let me know, and I will do my best to fix it promptly.

NOTE: This information and software are for educational purposes only and should not be used in place of services from a professional appraiser. Formulas cannot be 100% accurate due to subtleties not included in the formulas. All decisions should be based on your own knowledge. I cannot accept any responsibility for decisions you make.

Thank you for visiting FOLDS.NET.
Copyright 1995-96, 2001-02 by Jasper Paulsen.
Your comments are welcomed.
Begun August 2001. This page was first posted September 24, 2001.
This page includes text first posted September 15, 2001.
Last updated October 22, 2003.